Introduction to the Theory of Everything.
Basic definitions.
There are: 3d space, matter only as infinitely tiny uniform particles, each representing smallest possible mass, with simple mechanical traits of motion (only along straight line) and interaction.
No limit on size of space/universe and speed of particles.
Obviously, this assumes that universe is fully deterministic.
Gravity.
There was lots of attempts to explain gravity from point of mechanical interaction of particles, and lots of models stand pretty close, but, by some reason those models (and researchers) were considering exactly separate particles and there was missed one critical thing, which is the following:
two/many tiny simplest particles can stand nearby each other and move (as closely standing group of particles) along the same direction (what should be correct situation from point of any theory of explanation of the world), and what is core of the answer.
They are not glued, don't have any complex interaction among them, etc, and simply stand nearby (or move at the same direction).
During collision of such group with other particle or group of particles interaction happens strictly according to simplest rules (of mechanics). During interaction group of particles can be split into several smaller groups of particles. In case particles at the group stand one behind each other then such particles act as single mass.
Everything described is obvious simplest mechanical traits and interactions.
And actually how gravity works with nearby standing particles taken into account.
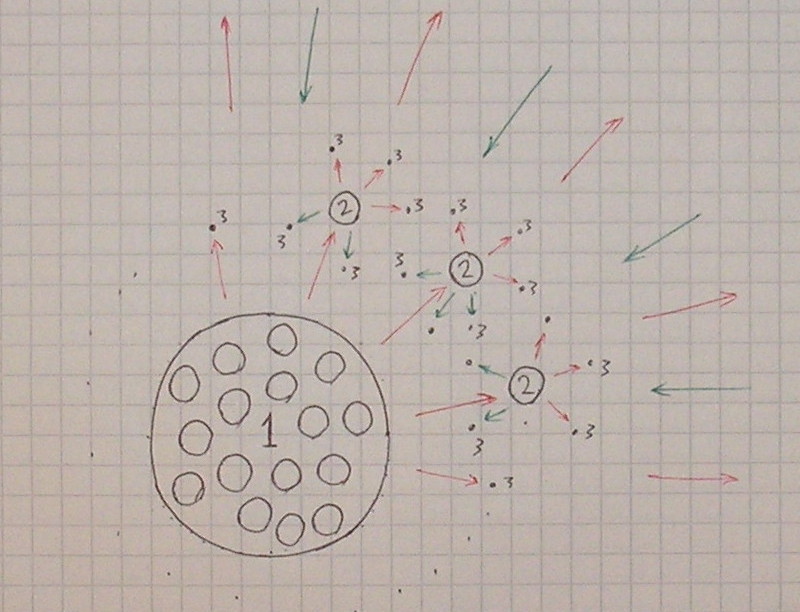
Large groups of nearby standing particles (with the same speed and direction of motion) from time to time collide with other particles and groups of particles (randomly moving around at space).
During interaction larger group gets smaller speed, smaller group (or separate particle) gets higher speed. Group of particles can be split into peaces which get momentum according to the same principle.
Group of initial participants starts to form larger amount of split groups and this forms cloud of interacting particles and groups of particles.
Interacting in such a cloud, smaller groups of particles receive greater speed and are more likely to fly out of the group, but as they fly away, they give up their momentum towards the center and thus restrain the group, by pushing particles and groups of particles to the center.
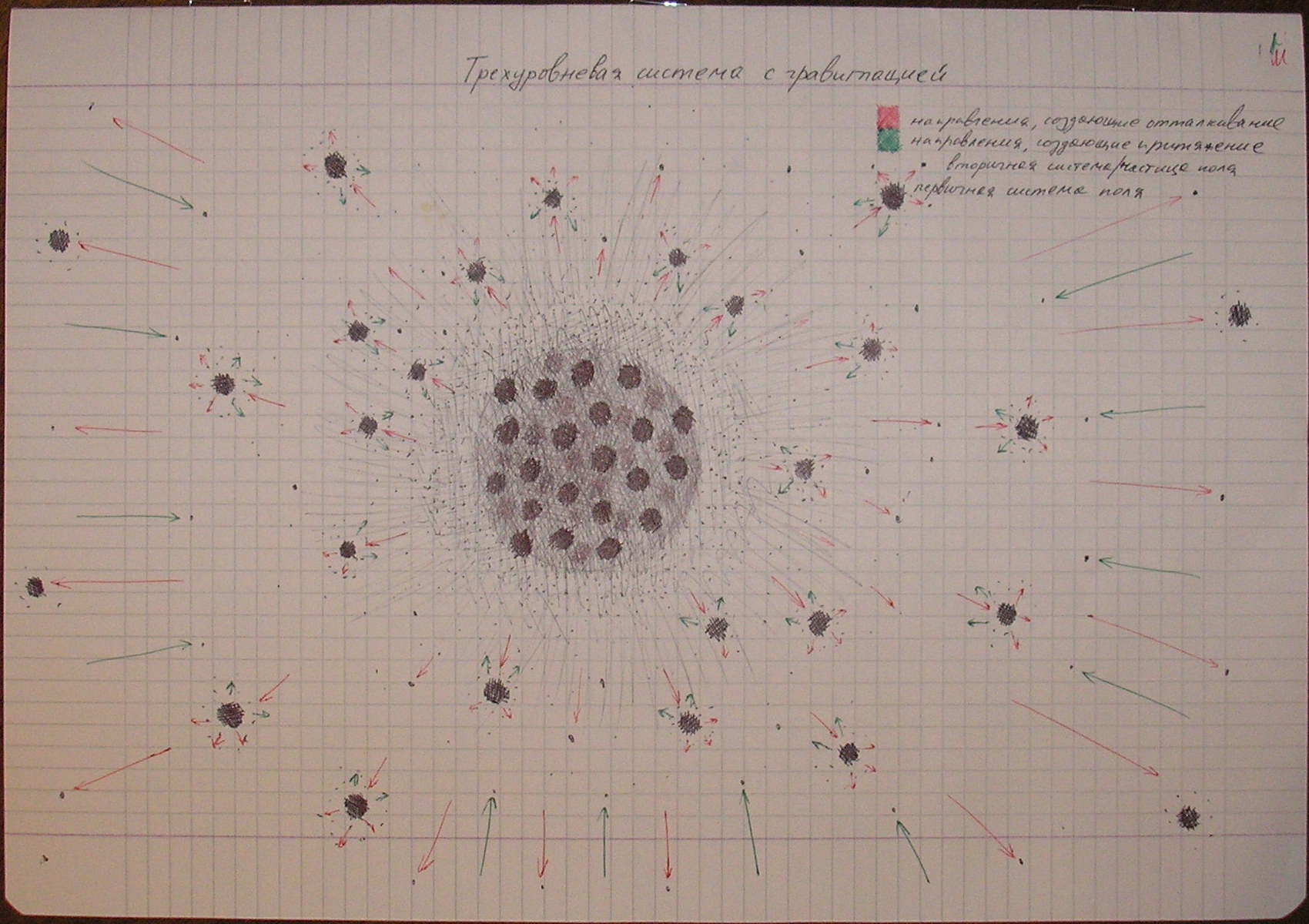
This system is a particle system with a repulsive field.
When colliding with a similar system in space, they smoothly transfer momentum to each other through the repulsive field and can interact without destruction of the structure.
Further similar systems of particles can form by the same principle more complex systems consisting not of the simplest particles and systems of particles, but of systems of particles with a repulsive field described above, which in the same way restrain the group by transferring momentum towards the center when flying away from the group.
Such system is already a system of particles with a gravitational field, which operates according to the following principle:
By flying away from the group and moving away to infinity, the particle system with a repulsive field constantly sends a stream of the simplest particles and groups of nearby standing particles in all directions, and the particle flow that is directed back to the main group creates a gravitational attraction to the radiating body.
One of the key principles is that the smallest particles and groups of particles which fly away (according to the principles of momentum distribution) receive the highest speed, and thus the speed of the created field is very high compared with the radiating body.
This is the simplest description of gravity.
All other complex interactions are based on this simple scheme of interacting particles with a gravitational field.
Resolution of wave-particle duality.
The following scheme is used for reasoning:
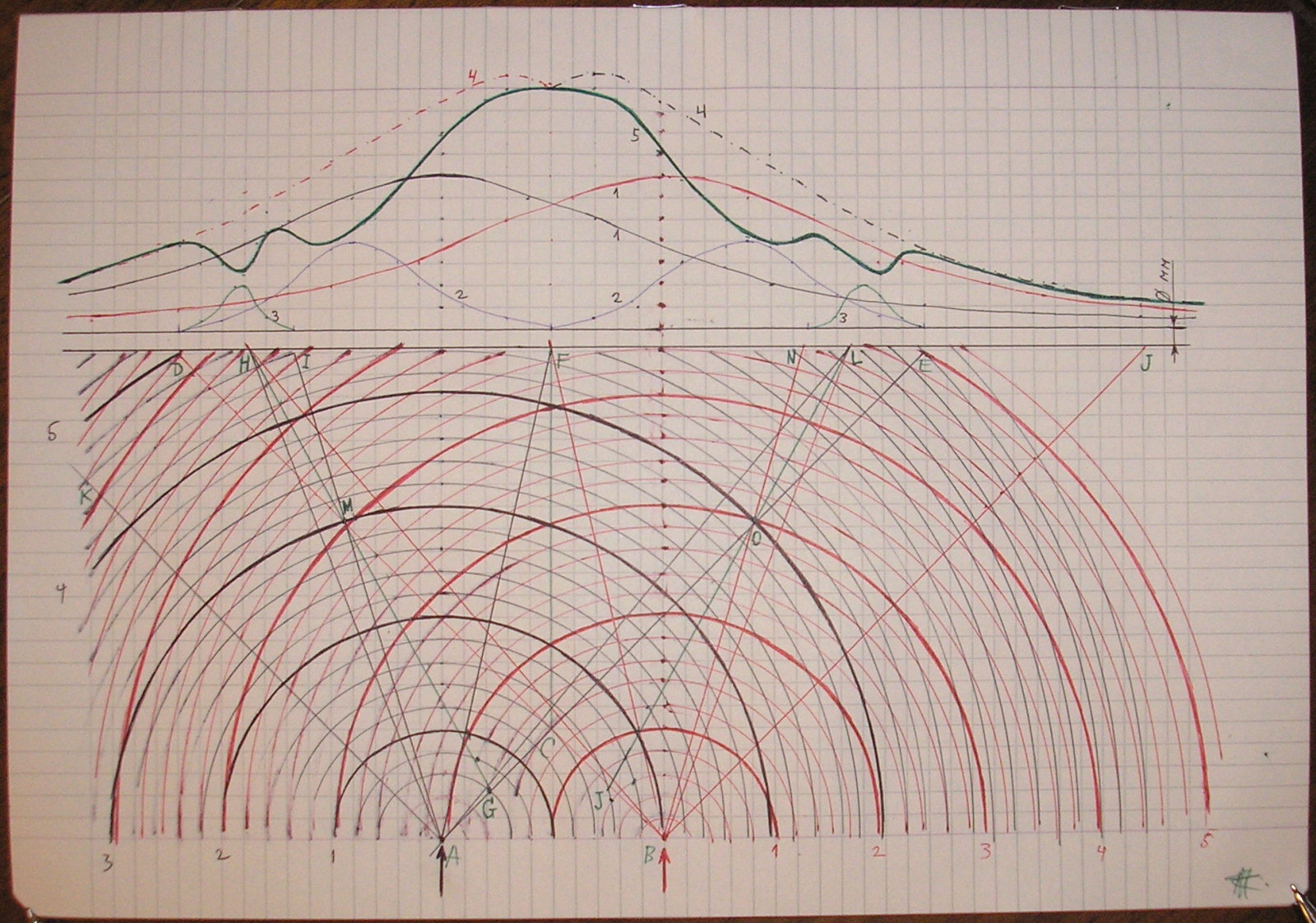
Let's consider how the wave interference by simple particles with the simplest mechanical interactions is formed, which will be the resolution of wave-particle duality in favor of particles.
The letters A and B indicate the holes at the bottom of the wall and the arrows below indicate the particle flows.
The first key point in this process is the following:
- When the flow passes through the hole, a part of the particles collides with the edges and/or walls of the hole.
- Further, these particles introduce randomness of movement into the flow when they collide with other particles inside the flow (which could have had already some level of randomness of internal movement before that).
Thus, instead of one direction, a certain distribution of directions is formed at the exit from the hole, which is indicated in the figure by a divergent semicircle, or in other words a "wave" of particles is formed.
Accordingly, the two holes form two diverging waves of particles, which, obviously, interact one with the other by particles with a certain probability.
In this case, the radiation period of the waves is equal to one cell of the notebook.
All waves are identical and some of them are marked by bold solely for the purpose of simplifying the analysis of the picture, which are also named by numbers.
Let's consider the interaction of the black wave number 1 and the red wave number 1.
The main area of interaction is along the C-F line, where the particles of the waves intersect with each other and where the particles, when collide with some probability. The collided particles do not leave an expressed mark on the screen but fly away in random directions.
The main interaction occurs in the region of maximum density of particles in the wave.
Also has to be taken into account the fact that the farther from the main direction, the smaller the density of particles in the wave, and in the directions close to 90 degrees the number of particles tends to zero.
The maximum interaction would have to start at the very bottom relative to the C-F line (below point C), but there are almost no particles and the number of interactions is minimal.
Further, as the interaction point moves upwards, on the one hand, the density of the wave increases due to approaching the main direction, on the other hand, at some point the density begins to decrease with increase of distance from the point of radiation due to dependence of density on distance (from radiation point) by a pattern similar to the inverse square law.
It can be assumed that the maximum density of particles of the wave (in the interacting part of the wave) is somewhere in the middle of the line between points C and F.
It should also be noted that the point of interaction on the arc of the wave is constantly shifting, which is obvious as the angle from the point of radiation to the point of interaction changes with movement upward.
This interaction will have the following effect on the screen:
each of the waves interacts only by its part up to the point F, where the right wave does not interact with the part from point F and to the right and interacts with the part from point F and to the left, where the entire left side on the screen will be a projection of its interaction with another (left) wave, where the distribution of activity of interaction will be reflected as described above, but at the screen this will be reflected in the reverse way:
at the point of maximum interaction (somewhere in the middle, where the density of particles is maximal), the number of lost particles will be maximal, and it decreases as it moves to points F and C.
Accordingly, the schematic graph #2 on the left side of point F indicates the number of lost particles on the screen by the right wave, which reflects maximal loss of the particles in the center of interaction.
Likewise, everything happens for the left wave, only in a symmetric way, and it does not interact with its left part, and on the right side loses particles just like the right wave to the left, and in graph #2, to the right of F is indicated loss of particles by the left wave.
Thus, graph #2 shows the distribution of lost particles in the interaction of the two considered waves.
Next, we consider the interaction of waves released at different points in time using the example of the interaction of black wave #1 and red wave #2.
Their interaction starts from the bottom left at point 1 (which is also the name of one of the first black waves), where, due to the large radiation angle, it is almost absent, and increases with upward movement, where the point M is supposed to be the point of maximum interaction, what is reflected on the graph #3, where the D-I section is the projection of the span of the maximum interaction of waves, where H is the projection of the peak of interaction with the maximum loss of particles.
The graphs are schematic and approximate, drawn to reflect the essence of the process.
Next, we find the result of the considered interactions by their expression at the screen.
Two graphs with the number #1 show how the captured patterns of the waves for each hole separately should look like.
Chart #4 is the sum of the (4) waves without taking into account their interaction (in this scheme, the addition of these graphs is not perfectly correct, where the resulting graph should be much higher).
Further, from this graph have to be subtracted all the lost particles indicated by the graph #2 and #3.
The resulting graph #5 shows the obtained interference pattern for the considered waves.
When considering and adding all interacting waves, the overall picture of interference will be more complex.
Law of nature.
The rest of the main book examines the main areas and phenomena of physics and provides hypothetical schemes for how it all works based on the Theory of Everything and the mechanics of gravity.
Initially, when developing the Theory of Everything and finding out how well-known phenomena correspond to the described gravity scheme, the systematic approach was not used and the problems were considered intuitively, but after explaining several complex phenomena, this transformed into a simple straightforward approach with breaking the problem into parts and as a result this approach was formulated in the form of the following principle:
If there is something complicated, then there is something simple of which this complex consists.
In explaining complex physical phenomena, it works so reliably that this principle was raised to the "law of nature."
Further, it was simplified to the phrase "a complex consists of a simple" and then even further to a single word: simplicity,
which is the main and the only law of nature.
This principle works so smoothly and builds so perfect a physical understanding of the world that everything that contradicts this principle at the basis of physical perception can be either decomposed into simpler components, or it can be discarded as incorrect.
Matter is represented as an infinitely small particle with the simplest properties of the motion and interaction.
The space is 3-dimensional.
Time is homogeneous.
When using Theory of Everything and understanding of the correct scheme of gravity, a lot of "complex phenomena" and unsolvable problems become simple and obvious.
Let's consider, for example, the concept of energy that drives all the surrounding processes and how long the environment can exist based on the reserve of this energy.
Energy is represented by groups of nearby standing particles which, by colliding, transfer a larger momentum to smaller groups or to particles and accelerate them and thus create a repulsive field for the simplest particle system with a field, where high velocity of the field is a critical factor for the existence of gravity.
Thus, the process of decay of systems of nearby standing particles during collisions is the process of "energy burning". When such groups of particles disintegrate to a (average) size that will be unable to accelerate the field to the required speed to create gravity, this will lead to a gradual disintegration of the complex structures of matter.
Since the simplest particle has an infinitely small size and mass, then in such basic groups of nearby standing particles, which represent stored in such a way energy, the number of simplest particles can be considered as infinitely large.
Considering that the speed of the field is finite and the processes around run at a finite speed, the decay of such groups of particles will take a very long time (for us this can be considered as infinity).
And so on. The book and the article on gravity contain more information about the description of the world based on the Theory of Everything.


